 |
Chapter 4 Expressions |
 |
The multiplicative operators in Java are binary operators that are used for multiplication (*), division (/), and the remainder operation (%). The multiplicative operators appear in multiplicative expressions:
![[Graphic: Figure from the text]](figs/jlr0415.gif)
The multiplicative operators are equal in precedence and are evaluated from left to right.
References Unary Operators; Order of Operations
The binary multiplication operator * produces a pure value that is the product of its operands. The * operator may appear in a multiplicative expression. The multiplication operator never throws an exception.
Here is an example that uses the multiplication operator:
int doubleIt(int x) {
return x*2;
}
The types of both operands of the multiplication operator must be arithmetic types, or a compile-time error occurs. The * operator may perform type conversions on its operands:
If the multiplication of integer data overflows, the low order bits of the product are returned; no exception is thrown. The most significant bit of the low order bits is treated as a sign bit. When overflow occurs, the sign of the number produced may not be the same as the sign of the mathematically correct product, due to the limitations of the two's complement representation used for integer data.
The multiplication of floating-point data is governed by the following rules:
References Arithmetic Types
The binary division operator / produces a pure value that is the quotient of its operands. The left operand is the dividend and the right operand is the divisor. The / operator may appear in a multiplicative expression.
Here is an example that uses the division operator:
int halfIt(int x) {
return x/2;
}
The types of both operands of the division operator must be arithmetic types, or a compile-time error occurs. The / operator may perform type conversions on its operands:
The division of integer data rounds toward zero. If the divisor of an integer division operator is zero, an ArithmeticException is thrown. If the dividend is Integer.MIN_VALUE or Long.MIN_VALUE and the divisor is -1, the quotient produced is Integer.MIN_VALUE or Long.MIN_VALUE, due to the limitations of the two's complement representation used for integer data.
The division of floating-point data is governed by the following rules:
References Arithmetic Types; Integer; Long; Runtime exceptions
The binary remainder operator % produces a pure value that is the remainder from an implied division of its operands. The left operand is the dividend and the right operand is the divisor. The % operator may appear in a multiplicative expression.
Here is an example that uses the remainder operator:
// format seconds into hours, minutes and seconds
String formatTime(int t) {
int minutes, seconds;
seconds = t%60;
t /= 60;
minutes = t%60;
return t/60 + ":" + minutes + ":" + seconds;
}
The types of both operands of the remainder operator must be arithmetic types, or a compile-time error occurs. The % operator may perform type conversions on its operands:
When the remainder operation is performed on integer data, the following expression is guaranteed to produce the same value as a%b:
a-((a/b)*b)
The sign of the value produced by the remainder operator is always the sign of the dividend. The magnitude of the value produced by the remainder operator is always less than the absolute value of the divisor. If the divisor is zero, an ArithmeticException is thrown.
Unlike C/C++, Java provides a remainder operation for floating-point data. The remainder of floating-point data is computed in a manner similar to the remainder of integer data. The remainder operation uses a truncating division to compute its value. This is unlike the IEEE 754 remainder operation, which uses a rounding division. The IEEE remainder operation is provided by the Math.IEEEremainder() method.
The computation of the remainder of double and float data is governed by the following rules:
p is the dividend and d
is the divisor. The notation 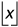 means the greatest integer less than or equal to
x ; this is called the floor operation.
means the greatest integer less than or equal to
x ; this is called the floor operation.
References Arithmetic Types; Math; Runtime exceptions
| This HTML Help has been published using the chm2web software. |